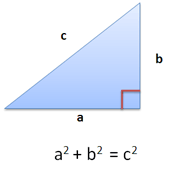
Teorema Pythagoras sering dianggap sebagai fakta tentang segitiga siku-siku.
Mari kita coba interpretasi yang lebih luas: Teorema Pythagoras menjelaskan bagaimana area 2D dapat digabungkan.
Inilah yang saya maksud. Misalkan kita memiliki dua garis tergeletak di sekitar (yang secara kreatif bernama Jalur A dan Jalur B). Kita dapat memutarnya untuk membuat area:
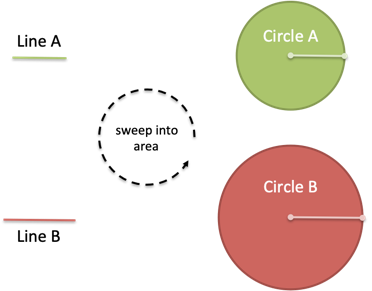
Oke, cukup menyenangkan. Dimana misterinya?
Nah, apa yang terjadi jika kita menggabungkan segmen garis sebelum memutarnya?
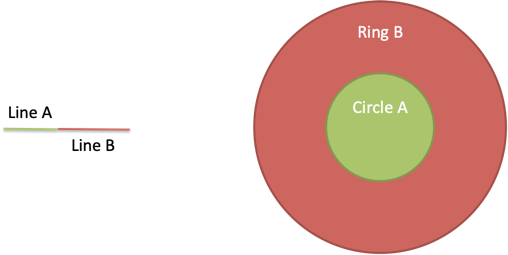
Wah. Area yang tersapu tampaknya berubah. Seharusnya bergerak garis, tidak memanjangnya, mengubah area?
Menjalankan Angka
Mengamati diagram di atas, sepertinya area itu tumbuh. Mari kita kerjakan secara spesifik.
Sebagai contoh, misalkan $a = 6$ dan $b = 8$. Ketika mereka disapu ke dalam lingkaran ($text{area} = pi r^2$) kita mendapatkan:
Untuk total $36pi + 64pi = 100pi$.
Segmen gabungan memiliki panjang $c = a + b = 14$, dan ketika kita memutarnya, kita mendapatkan:
Uh oh. Itu jauh lebih luas dari sebelumnya.
Masalah
Apa yang terjadi? Nah, Lingkaran A tidak berubah. Tapi Lingkaran B jauh lebih sedikit daripada Cincin B (lihat saja!).
Masalah: Saat Jalur B berputar sendiri, hanya bisa mencapai 8 unit saat menyapu. Ketika kita menghubungkan Jalur B ke Jalur A, itu mencapai 6 + 8 = 14 unit. Sekarang sapuan melingkar mencakup lebih banyak area, artinya Lingkaran B lebih kecil dari Cincin B.
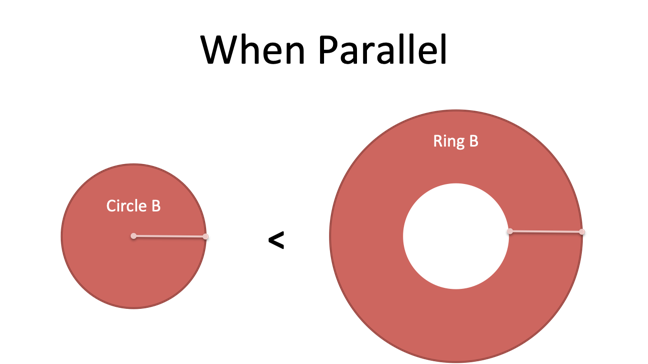
Secara matematis, inilah yang terjadi.
![displaystyle{underbrace{[a + b]^2}_{text{Lingkaran C}} = underbrace{a^2}_{text{Lingkaran A}} + underbrace{2ab + b^2}_{text{Ring B}} > underbrace{a^2}_{text{Lingkaran A}} + underbrace{b^2}_{text{Lingkaran B}}}” class=”tex”/></p>
<p>Abaikan $pi$ sejenak karena ini adalah istilah umum. Saat memperluas $c^2 = (a + b)^2 = a^2 + 2ab + b^2$, ada istilah $2ab$ baru yang harus pergi ke suatu tempat. Karena Lingkaran A tidak berubah, area tambahan ini harus muncul di Ring B.</p>
<h2>Membuat Hal-Hal Berbaris</h2>
<p>Itu… masuk akal jika area itu berubah, tapi aku tidak menyukainya. Hanya memindahkan barang-barang di sekitar seharusnya tidak memiliki efek ini! Bisakah daerah itu sama?</p>
<p>Tentu, jika kita menghapus istilah $2ab$. Perbaikan mudahnya adalah mengatur $a=0$, tapi itu curang dan Anda tahu itu.</p>
<p>Mari kita cari solusi cerdas. Secara intuitif, pertanyaannya adalah: <strong>Bagaimana panjang Garis A? <em>bukan</em> membantu Jalur B saat berputar?</strong></p>
<p>Miringkan! Saat kita memutar Jalur B, ada sedikit manfaat dari panjang Jalur A. Tangga tidak berguna saat berbaring di lantai, bukan?</p>
<p><picture><source srcset=](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/570b9a017be116fe0c695ad715899195.png)
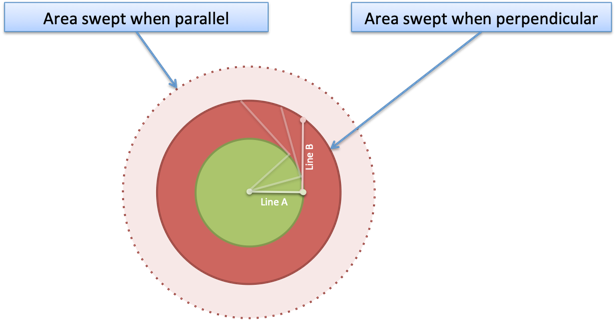
Ketika kita menggunakan Full Perpendicular™, suku $2ab$ menghilang dan Lingkaran B = Ring B. (Dalam istilah vektor, produk titik adalah nol: $a cdot b = 0$).
Ah — itulah arti dari Teorema Pythagoras. Ketika segmen garis tegak lurus, area yang sama disapu apakah garis digabungkan atau dipisahkan.
Memeriksa Matematika
Ini bukan ide yang buruk untuk memastikan nomor berbaris.
Karena segmen sekarang tegak lurus, kita tahu $c^2 = a^2 + b^2$, jadi:
Sekarang kita dapat menghitung:
Tada! Cincin dan Lingkaran menyapu area yang sama.
Dalam contoh kita, kita memiliki Lingkaran A = $36pi$, Lingkaran B = $64 pi$, $c = sqrt{36 + 64} = 10$. Lebar cincin adalah $10 – 6 = $4.
Ringkasan
Teorema Pythagoras lebih dari sekadar segitiga. Ketika komponen tegak lurus, area yang mereka buat tidak tergantung pada bagaimana mereka diatur.
Lampiran: Aneka Pikiran
- NS Hukum Kosinus secara eksplisit menunjukkan suku $2ab$ yang diasumsikan nol dalam Teorema Pythagoras. Luas Ring B bahkan bisa menjadi “negatif” jika kita memiringkan Garis B agar mengarah ke dalam.
- Kami dapat menggabungkan area dari beberapa dimensi ($x^2 + y^2 + z^2 + …$). Selama saling tegak lurus, luas yang disapu oleh setiap dimensi adalah luas yang disapu oleh total.
- Teorema Pythagoras adalah hubungan dalam domain area 2D ($c^2 = a^2 + b^2$). Kita mulai di sini dan mengonversinya menjadi hubungan dalam domain 1D ($c = sqrt{a^2 + b^2}$). Konversi terjadi begitu sering kita lupa di mana itu dimulai.
- Lebih lanjut tentang menyapu area: https://www.cut-the-knot.org/Curriculum/Geometry/PythFromRing.shtml
Selamat matematika.
